QC検定3級を超重要分野「QC7つ道具」があります。
その「QC7つ道具」の中でも最も出題率の高いのが「管理図」です。
その次に重要なのが「散布図」です。
本記事では、「散布図」の例題を通して基本事項を確認できるようにまとめました。
それでは、実力チェック問題からどうぞ!
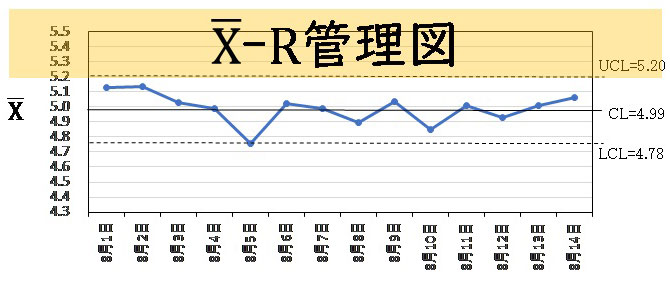
管理図の基礎確認はコチラ
目次
実力チェック問題(QC検定3級の散布図例題)
QC検定3級レベルの散布図の例題です。
問1、問2が簡単に解ければおそらく3級は合格できると思います。
(問2は頭の中で「あの公式使うんだよなぁ」というのがわかればOKです。ただし、試験本番では公式を覚えておく必要有りです)
では、解いてみてください!
実力チェック問題の解答
先ずは回答です。
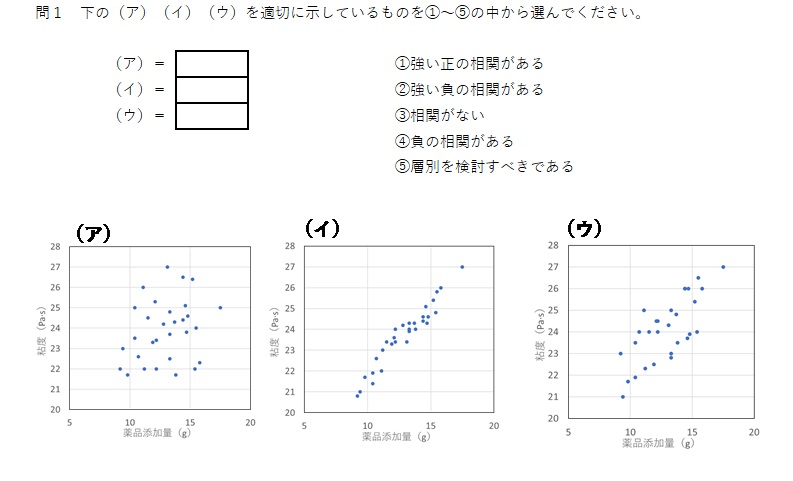
(ア)③ (イ)① (ウ)⑤
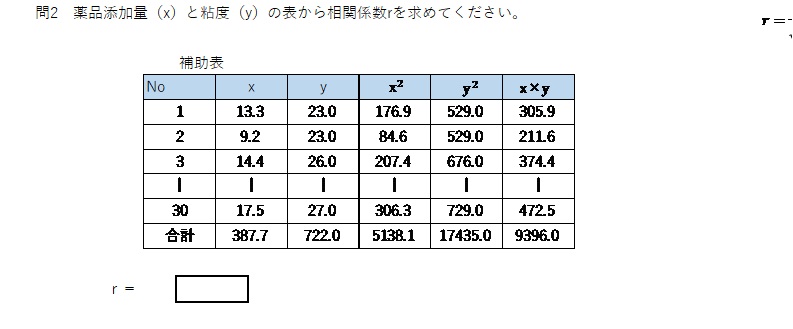
問2 r=0.75
問1の解説(散布図の型)
解説の前に散布図の基礎を抑えながら解説します。
(ほぼ解説してないですが)
散布図とは
原因と結果の2変数について関連性(関係)を明らかにするのが散布図です。
例えばこんな感じ、
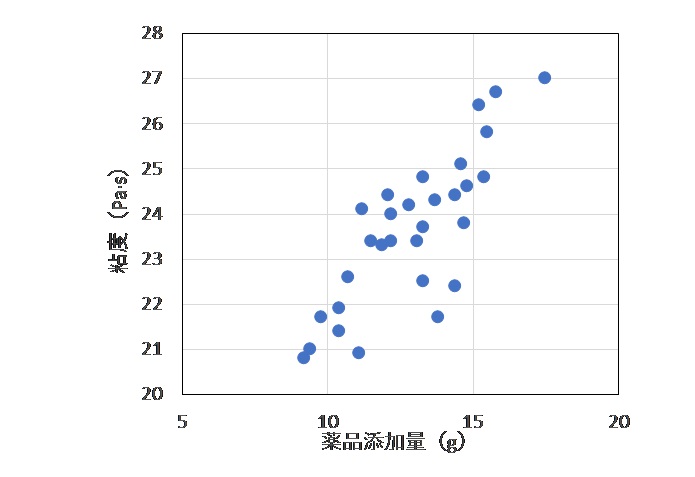
この場合だと、原因が「薬品添加量」で結果が「粘度」になりますね。
・データ数は少なくとも30組以上は必要です(少ないと誤った判断をする可能性が高くなります)。

散布図の見方
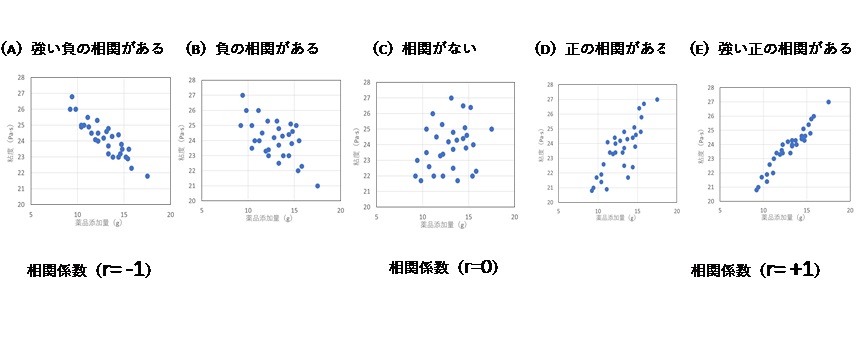
散布図の基本5パターン
(B)xが大きくなると、だいたいyも小さくなる
(C)xとyの間に何の関係もない
(D)xが大きくなると、だいたいyも大きくなる
(E)xが大きくなると、yも大きくなる

散布図の落とし穴
散布図の落とし穴というか、作成後の注意点があります(試験にも出ますよー)。
層別したら相関あり(orなし)のパターン
まずは層別。超重要です。
下の例は左の図を見ると「相関なさそう」ですが、層別したら「相関がありそう」になる例です。
(薬品A,Bで層別しましたが、他にもlotや作業者による層別が考えられます)
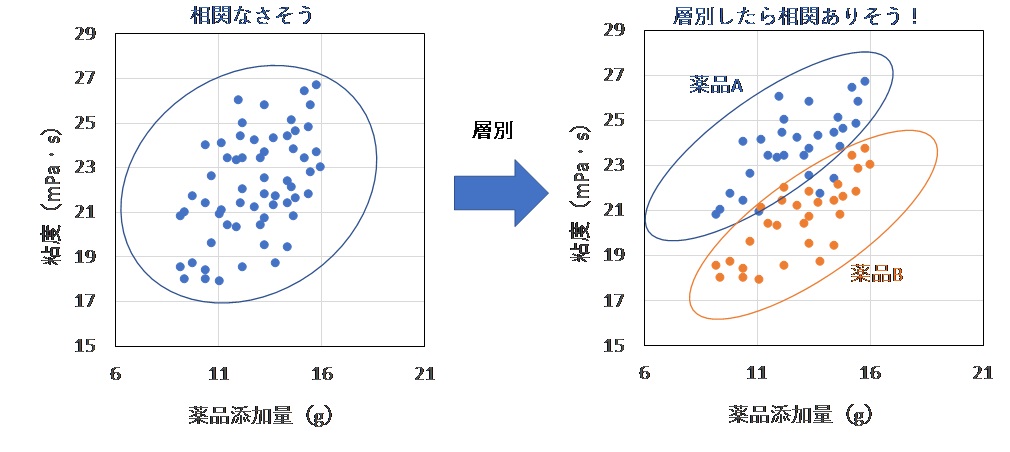

実力チェック問題の問2(ウ)がこのパターンですね。
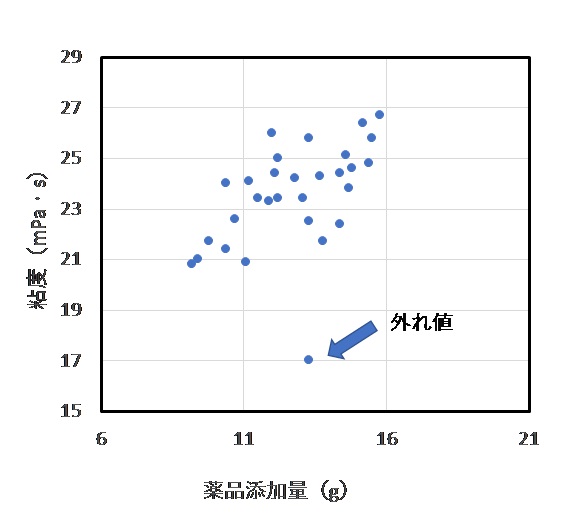
外れ値
実務で散布図を使う人は「あるある」だと思います。
対策としては、
・原因がわかっているなら外れ値を「取り除き」ます。
・原因がわからないなら外れ値も考慮する必要があります。

偽相関
最後は、偽相関(ぎそうかん)です。
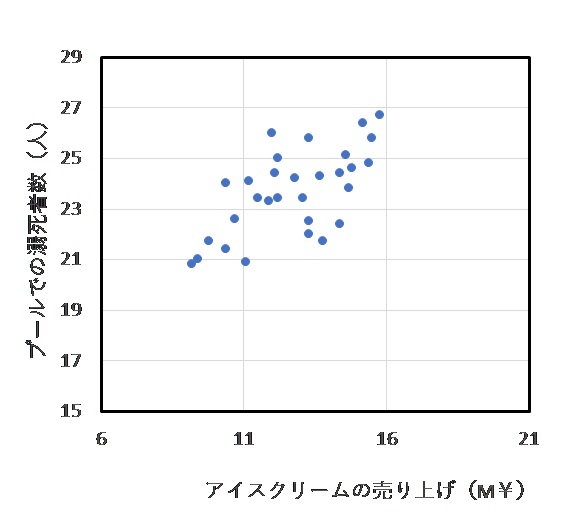
アイスクリームの売り上げが増えると、プールでの溺死者数が増える。っていうやつ。
アイスの売り上げと溺死者数って関係ないですよね。
アイスが売れるということは、暑くてプールに行く人の数も増えそうですからね。
問2の解説(相関係数)
問題は問2ですよね。
2015年(9月)以降に出題範囲になった「相関係数」の問題です。
相関係数を求める問題は
公式を覚えていれば解けますし、覚えていなければ解けません。
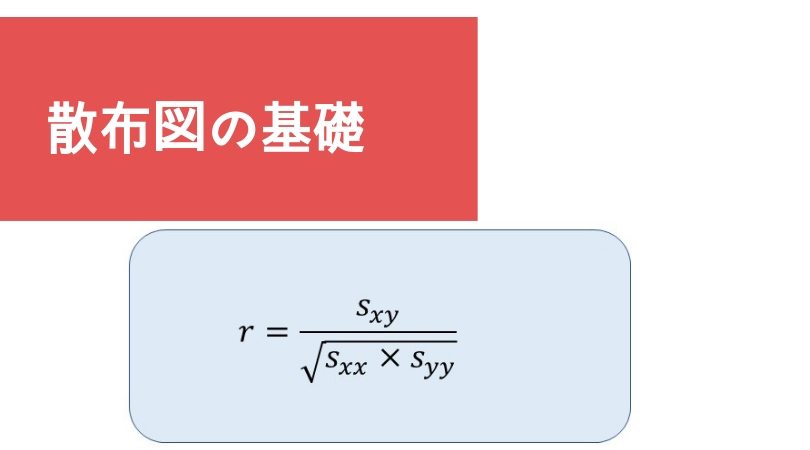
で、相関係数(r)を求める公式はコチラです。
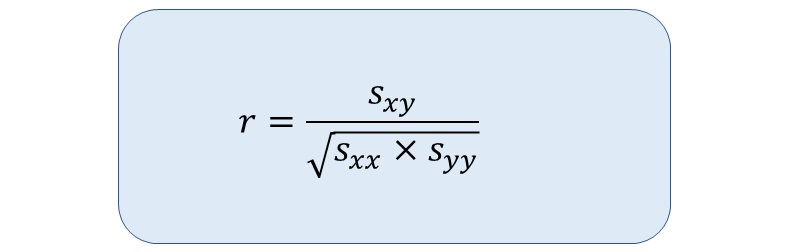
で、さらに、それぞれのSを求める式がコチラ。

シグマ(Σ)があると拒否反応出る人もいると思うので、Sxxだけシグマ無しで表記すると
こんな感じになります(赤枠の部分)。
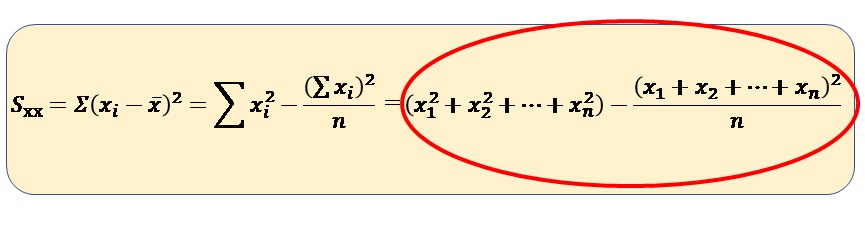
で、もう一度、相関係数を求める問題の補助表を見てみましょう。
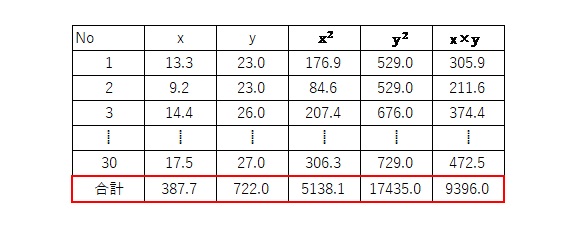
相関係数を求めるのに使うのは、赤枠の部分だけ!
実際に公式に当てはめてみましょう。

で、相関係数(r)を求めて終了。


まとめ
・2015年(3月)までは「散布図の型」だけ覚えておけばでよかった
・2015年(9月)以降は「相関係数を求める問題」も出題される(範囲増えた)。
・まずは「散布図の型」を覚える。余裕があれば「相関係数を求める公式」も覚える!